GEOMETRÍA ANALÍTICA (CÓNICAS)

GEOMETRÍA ANALÍTICA:

CÓNICAS:

• se le denomina sección cónica o (simplemente cónica) a todas la curvas de intersección entre un cono y un plano, si dicho plano no pasa por el vértice se obtiene las cónicas propiamente dichas se clasifican en tres tipos:

1. elipse 
2. parábola
3. hipérbole

 ELIPSE:

• le denominamos elipse al lugar geométrico de los puntos de un plano cuya suma de distancia a dos puntos fijos del plano es constante
• la excentricidad de una elipse es el grado de achatamiento y su valor esta determinado por la expresión:

1. cuanto mayor sea la excentricidad mas achatada es la elipse. en una elipse a>c>0 por lo tanto la excentricidad es positiva y menor que uno.

  ECUACIÓN:supongamos que el origen de las coordenadas esta en el centro de la elipse coinciden con el eje entonces los focos son:

                     F1 = (-C,0)      Y        F2 = (C,0)

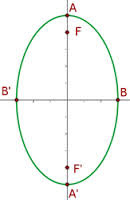
  ELEMENTOS DE LA ELIPSE:

1. FOCOS: son los puntos fijos F Y F 
2. EJE FOCAL: es la recta que pasa por los focos 
3. EJE SECUNDARIO: es la mediatriz del eje FF 
4. CENTRO: es el punto de intersección de los ejes 
5. RADIOS VECTORES: son los segmentos que van desde un punto de la elipse a los focos PF
6. DISTANCIA FOCAL:  es el segmento FF de longitud 2c, c es el valor de la semidistancia focal
7. VÉRTICES : son los puntos de intersección de la elipse con los ejes A,A , B Y B 
8. EJE MAYOR : es el segmento AA de longitud 2a , a es el valor del semieje mayor 
9. EJE MENOR : es el segmento BB de longitud 2b , b es el valor del semejante menor 
10. EJES DE SIMETRÍA : son las rectas que contiene al eje mayor o al eje menor 
11. CENTRO DE SIMETRÍA : coincide con el centro de la elipse, que es el punto de la intersección de los ejes de simetría 

  EXCENTRICIDAD DE LA ELIPSE: 

• la excentricidad es un numero  que mide el mayor o menor achatamiento de la elipse, y es igual al cociente entre su semidistancia focal y su semieje mayor 

                           e= c/a        c>a           0<e<1                                      c = 0  
                                                                                                              b = a
                                                                                                              e = 0 

ECUACIÓN REDUCIDA DE LA ELIPSE:

• en esta se toma el centro de la elipse como el centro de las coordenadas y los ejes de la elipse como ejes de coordenadas las coordenadas de los focos son: 

   F'(-c,0) y F(c,0)    
   Cualquier punto de la elipse cumple: 
   
  
   Esta expresión da lugar a:

    

      Realizando las operaciones llegamos a:

      

ECUACIÓN REDUCIDA DE EJE VERTICAL DE LA ELIPSE:

si el eje vertical esta en el de las coordenadas se obtiene una ecuación 

ECUACIÓN DE LA ELIPSE:

• si el centro de la elipse c(X0, Y0) y el eje principal es paralelo a 0x, los focos tienen de coordenadas F(X0+C, Y0) y F(X0-C, Y0)

ECUACIÓN DE EJE VERTICAL DE LA ELIPSE:

• si el centro de la elipse c(X0,Y0) y el eje principal es paralelo 0Y, los focos tienen de coordenadas F(X₀, y+c) y F'(X₀, y₀-c).y la ecuacion de la elipse sera: 

DEFINICIÓN ECUACIONES TRIGONOMÉTRICAS

ECUACIONES TRIGONOMÉTRICAS:

• en las ecuaciones trigonométricas intervienen funciones trigonométricas, que son periódicas y por lo tanto sus soluciones se pueden presentar en uno o en dos cuadrantes y ademas se repiten en todas las vueltas

para resolver una ecuación trigonométrica haremos las transformaciones necesarias para trabajar con una sola función trigonométrica para esto vamos a utilizar las identidades trigonométricas fundamentales 

        ejemplos:

                                cot(al cuadrado)x-2csc(al cuadrado)x+5=0           en el intervalo (0°,360°)

                                 cot(al cuadrado)x-2(cot(al cuadrado)x+1)+5=0

                                    cot(al cuadrado)x-2cot(al cuadrado)x-2+5=0

                                                                     -cot(al cuadrado)x+3=0

                                                                               -cot(al cuadrado)x=-3

                                           

                                                                                      cot(al cuadrado)x=3

                                                                                       tan(al cuadrado)x=1/3 

                   30°  = I                                                                 tanx=+(raíz cuadrada)1/3

                   150°= II

                   210°=III

                   330°=IV

• Después de que expresamos la ecuación en términos de una sola función trigonométrica, aplicamos los pasos usuales en la solución de ecuaciones algebraicas para despejar la función, por ultimo resolvemos la parte trigonométrica, es decir conociendo el valor de la función trigonométrica de una angulo hay que pasar a determinar cual es ese angulo.

ECUACIONES TRIGONOMÉTRICAS DE LA FORMA F(X)=K: 

DEFINICIÓN:

•       las ecuaciones de la forma f(x)=k donde f(x) es una función trigonométrica y k es una constante son aquellas ecuaciones en las que podemos encontrar la solución mas simple dado que las podemos utilizar realizando simples despejes, después de esto se emplea una identidad básica y luego el uso de la calculadora al final de esto hay que determinar el rango de la función ya que si K no pertenece a dicho rango la ecuación no tiene solución 
• en algunas ocasiones la ecuación puede venir escrita con diferentes funciones trigonométricas, por lo tanto tenemos que emplearlas identidades trigonométricas básicas hasta que la ecuación se encuentre escrita en términos de una sola función luego aplicamos despejes y la calculadora.

    EJEMPLO:

                           2CSC X +4=0                    en el intervalo(0°,360°)

                          

                               2CSC X= -4                     

                           CSC X = -4/2                  hay una identidad reciproca que me dice:sen x =1/ csc x

                               CSC = -2                             es decir, seno equivale al reciproco de la csc

     

                            SEN X = -1/2 _____III C =180°+30° = 210°                   X=(210°,330°)

                                                   _____IV C =360°-30° =330°

                                                                  

      para establecer el valor o valores de los ángulos solución es necesario realizar procesos de despejes de términos, factorizacion, simplificaciones, entre otros.

ECUACIONES TRIGONOMÉTRICAS LINEALES:

DEFINICIÓN: 

una ecuación lineal o de primer grado es en la cual solo involucramos sumas y restas de variables elevadas a la primera potencia (elevadas a uno,las cuales no se escriben)

• son llamada lineales porque se pueden presentar como rectas en el sistema cartesiano 
• se denomina ecuación lineal aquellas que tiene un polinomio de primer grado, es decir, las incógnitas no están elevadas a ni multiplicadas entre si, ni el denominador 
• como es bien sabido las ecuaciones lineales con 2 incógnitas representan una recta en el plano cartesiano

       ejemplo:

                   -X+2Y=3 

     pasos para resolver una ecuación lineal:   

1. se reducen términos semejantes cuando es posible 
2. se hace la transposición de términos 
3. se reducen términos semejantes hasta donde sea posible 
4. se despeja la incógnita dividiendo ambos miembros de la ecuación y se simplifica 

     ejemplo:

                      X+2=3                                              x=primer miembro

                                                                               3=segundo miembro

ECUACIONES TRIGONOMÉTRICAS EN FORMA FACTORIZADA:

FORMA POLINOMICA:

• se llama así porque la función esta expresada por un polinomio 

    ejemplo:

                      f(x)=ax(al cuadrado)+bx+c

FORMA FACTORIZADA:

• toda función cuadrática la podemos factorizar en función de sus raíces, dada:

     ejemplo:

                       f(x)=ax(al cuadrado)+bx+c

• siendo a el coeficiente principal de la función, por ellos extraemos siempre como factor común, de no escribirse el coeficiente de x(al cuadrado) seria siempre 1, X1 y X2 representan las raíces de f(x), en el caso de que el discriminante a sea igual a 0 entonces X1 = X2 , por lo que la podríamos escribir:

                       F(X)= A(X-X1)(al cuadrado)

•  en este caso a X1 se le denomina raíz doble ya que su orden de multiplicidad es 2 

FORMA CANÓNICA:

• toda función cuadrática la podemos expresar mediante el cuadrado de un binomio de la siguiente manera:

     ejemplo:

                                 f(x)=a(x-h)(al cuadrado)+k 

• siendo a el coeficiente principal y el par ordenado (H;K) las coordenadas del vértice de la parábola. para llegar a esta expresión se parte de la forma polinomica y se completan cuadrados. 

ECUACIONES TRIGONOMÉTRICAS CON IDENTIDADES: 

• el concepto de identidades trigonométricas es un concepto que utilizamos en el ámbito de las matemáticas para hacer referencia a las funciones trigonométricas variables. 
• las identidades trigonométricas pueden ser definidas en términos generales como todas las variables de un angulo que puede existir en una figura geométrica 

IDENTIDADES TRIGONOMÉTRICAS:

• son igualdades que involucran funciones trigonométricas, estas identidades son útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualquiera que sean los valores que asignen a los ángulos, para los cuales están definidas estas razones 

• una identidad trigonométrica es una igualdad entre expresiones que contiene funciones trigonométricas y es valida para todos los valores del angulo en los que están definidas las funciones (y las operaciones aritméticas involucradas)
• explicación de todas las funciones en 0 (cero)

HOMOTECIAS

¿que es una homotecia?

Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. En general una homotecia de razón (λ) diferente de 1 deja un único punto fijo, llamado centro.

Se puede considerar a la homotecia una homología particular de eje impropio, con centro en el de homología.

Homotecia con centro O y λ>1

Las homotecias transforman una figura plana en otra figura de igual forma, pero de menor o mayor tamaño, según el valor de la razón, k. Si kes positivo la homotecia es directa, y si no, es inversa. 

Homotecia directa y homotecia inversa

• Si k > 0, A y A′ están al mismo lado de O, y se dice que lahomotecia es directa.

• Si k < 0, A y A′ están a distinto lado de O, y se dice que lahomotecia es inversa.

A la figura ABC le hemos aplicado una homotecia de centro O y razón k, con k < 0; homotecia inversa.

En una homotecia de centro el punto O y razón k:

A la figura ABCD le hemos aplicado una homotecia de centro O y razónk, con k > 0; homotecia directa.

homotecia directa

homotecia inversa

Propiedades de las homotecias

1.^o Toda recta que pasa por el centro de homotecia es invariante, es decir, se transforma en sí misma.

homotecia recta

2.^o Toda recta que no pasa por el centro de homotecia se transforma en otra recta paralela a la dada.

3.^o La razón de dos segmentos homotéticos es igual a la razón k de la homotecia.

SEGMENTOS HOMOTETICOS

4.^o Una homotecia transforma los ángulos en ángulos iguales.

angulos homoteticos

• en el siguiente video podemos ver un ejemplo de homotecia directa o positiva:

• en el siguiente video podemos ver un ejemplo de homotecia inversa:

Caracteristicas:
1.- medidad proporcionales
2.-son semejantes
3.-angulos iguales
4.-son a escala

Tipos de homotecia:

1.-HOMOTECIA DIRECTA: es aquella en la cual el punto de homotecia o el centro de homotecia se encuantra despues o antes de la figura trazada. La caracteriztica principal es que los segmentos entre las figuras son paralelas.

2.-HOMOTECIA INVERSA: Es aquella en la cual el centro de homotecia se encuentra entre la figura.

La homotecia tambien puede ser positiva o negativa. Determinan la razon que se tome es decir, el factor principal por el cual se multiplica.
Para encontrar la razon de homotecia debe colocarse uno a uno cada lado o segmento de las figuras y sacar la constante de proporcionalidad. 

Sea k un número positivo, cuando aplicamos una homotecia de centro O y razón k a un punto cualquiera P, obtenemos otro punto P' de la semirrecta que definen O y P, de manera que

Al punto P' lo denominaremos homólogo de P.

Ten en cuenta que si k<1, el punto P' queda situado entre O y P.

También se pueden considerar homotecias en la que la razón sea negativa, en la  figura tienes el efecto de aplicar una homotecia de centro O y razón -2 al Triángulo ABC:

Cuando la razón es negativa, el centro de la homotecia queda situado entre el punto y su imagen.

ESTADISTICA

• 

¿que es la estadística?

La estadística es una ciencia matemática especializada en el análisis de grandes volúmenes de información para de ella extraer conclusiones. Tras analizar los datos deduce determinadas características de dicha información.

Se puede distinguir entre:

Estadística descriptiva: analiza un conjunto de datos y extrae conclusiones.

Ejemplo: se analiza la estatura y el peso de los alumnos de una clase y se determina cual es el valor medio, cuales son los máximos y los mínimos, cual son los valores más repetidos.

Estadística inferencia: en base a un conjunto de datos permite predecir cómo se puede comportar la variable en un futuro, o bajo determinadas circunstancias.

Ejemplo: se analiza una serie de variables económicas (consumo, renta, paro, etc.) y a partir de ahí se predice cual puede ser la evolución futura de la economía.

métodos numéricos para la caracterización de variables :

MEDIDAS DE LOCALIZACIÓN

Las medidas de localización dividen la distribución en pares iguales, sirven para clasificar a un individuo o elemento dentro de una determinada población o muestra.


Clasificación


Media: X = Σ xi   
                          n


Mediana: Pares  12345678 → 4+5 
                                                           2


                     Impares 1234567 → 4


Moda: Dato que mas se repite, puede ser de 3 formas:

• Modales: números que se repiten una sola vez   → 1223456789
• Bimodales: números que se repiten dos veces    →  12233456789
• Multimodales: números que se repiten mas de dos veces →1223344556789
• Amodales: Los números no tienes repeticiones  → 123456789

Percentiles: Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales.

i = P    . n

     100

Deciles: Deciles son los 9 valores que dividen la serie de datos en 10 partes iguales.

i = P    . n

      10

Cuartiles: Son los 3 valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales. Q1, Q2, Q3 determinan los valores correspondientes al 25%, 50% y 75% de los datos.

Q1 = 25     . n

          100

En el siguiente video podemos ver un ejemplo de como se calculan las medidas de localización:

MEDIDAS DE VARIABILIDAD Y DISPERSIÓN

Nos ayudan a determinar la variación de los datos y determinan como se agrupan o se dispersan los datos alrededor de un promedio.


Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptan dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (Desviación media) y otra es tomando las desviaciones al cuadrado (Varianza).


Rango intercuartil: Representa el 50% de los datos centrales

IQR = Q3 - Q1

Varianza: Sirve para comparar la variabilidad de dos o mas variables. La hay de dos tipos:

Muestral: S² = Σ(xi - X)²  

                        n-1

Poblacional: Õ² = Σ(xi -   )²  

                       N

Desviación estandar: Es una medida que informa de la media de distancias que tienen los datos repecto de su media aritmetica expresada en las mismas unidades que la variable.

Muestral: S = S²

Poblacional: Õ = Õ²

Punto Z: Determina que tan lejos esta un punto de la media y se calcula:

Z = xi - X   

           S

Campa de Gauss: La campana de Gauss es una representación gráfica de la distribución normal de un grupo de datos. Éstos se reparten en valores bajos, medios y altos, creando un gráfico de forma acampanada y simétrica con respecto a un determinado parámetro. El punto máximo de la curva corresponde a la media, y tiene dos puntos de inflexión a ambos lados.

Este gráfico se usa en variables asociadas a fenómenos naturales: caracteres morfológicos de individuos como la estatura o el peso, caracteres fisiológicos como el efecto de un fármaco, caracteres sociológicos como el consumo de un determinado producto por un mismo grupo de individuos,  caracteres psicológicos como el cociente intelectual.

Teorema de Chevichev: Permite conocer a cierta escala el comportamiento de sus individuos sabiendo la media y la desviación tipica.

1 - 1  

     Z²

Diagrama de Caja: Un diagrama de caja es un gráfico, basado en cuartiles, mediante el cual se visualiza un conjunto de datos. Está compuesto por un rectángulo, la "caja", y dos brazos, los "bigotes".

Es un gráfico que suministra información sobre los valores mínimo y máximo, los cuartiles Q1, Q2 o mediana y Q3, y sobre la existencia de valores atípicos y la simetría de la distribución.

Para el calculo de los "bigotes" se utiliza la siguiente formula:

Limite inferior: Q1 - 1,5(IQR)

Limite superior:  Q2 + 1,5(IQR)